6.5 Problem solving steps
6.5.1 Problem solving in general
We now have several different ways of determining the energy of some physical system—how do we actually use this knowledge to solve problems?
Solving physics problems is not about simply memorizing formulas. Instead, we focus on understanding a process. You will encounter different sorts of problems, where you will need to use different principles. We’re starting with conservation of energy, but later on we’ll encounter conservation of momentum (ch. 7 and ch. 8), Newton’s second law (ch. 9 and ch. 11), and kinematics (ch. 12). Very generally—for just about any problem you encounter—you’ll follow these three basic steps:
- Draw a picture.
- Apply a fundamental law or principle of physics.
- Solve.
Drawing a picture helps you visualize the situation that is presented in a problem. You should label your drawing with things like arrows to indicate motion, and variables representing physical quantities. Sometimes you’ll find drawing a sequence of pictures to be useful. Your drawing does not have to be an artistic masterpiece; it just needs to serve as a bridge between the verbal and mathematical explanations of a situation.
Recognizing which fundamental law or principle is one of the most important parts of solving the problem. This is your mathematical description of the situation and your starting point for actually solving quantitatively.
The final step is where you carry out the algebra required to get to an answer. You’ll always work from very general (a fundamental law or principle) to specific (what is going on in this particular situation). Remember to work symbolically, and save adding numbers until the very last step.
6.5.2 Solving problems with energy conservation
Section 6.1.1 gives us a mathematical statement of conservation of energy:
\[
E_i = E_f
\]
When we’re solving problems where energy is converted from one form to another, this is the fundamental law that we’ll apply to solve the problem.
Example 6.2
A cat is on a skateboard at the top of a ramp 2 m above the ground. If it starts from rest, what is its speed at the bottom of the ramp? Friction is negligible; it is small enough that it may be ignored.
Step 1: Draw a picture
In my drawing, I’ll represent the cat as a circle. I’ll use a solid black circle at the top of the ramp, and a gray circle to represent the cat once it has reached the bottom of the ramp. I have labeled the initial height and velocity, and the final velocity is represented by an arrow.
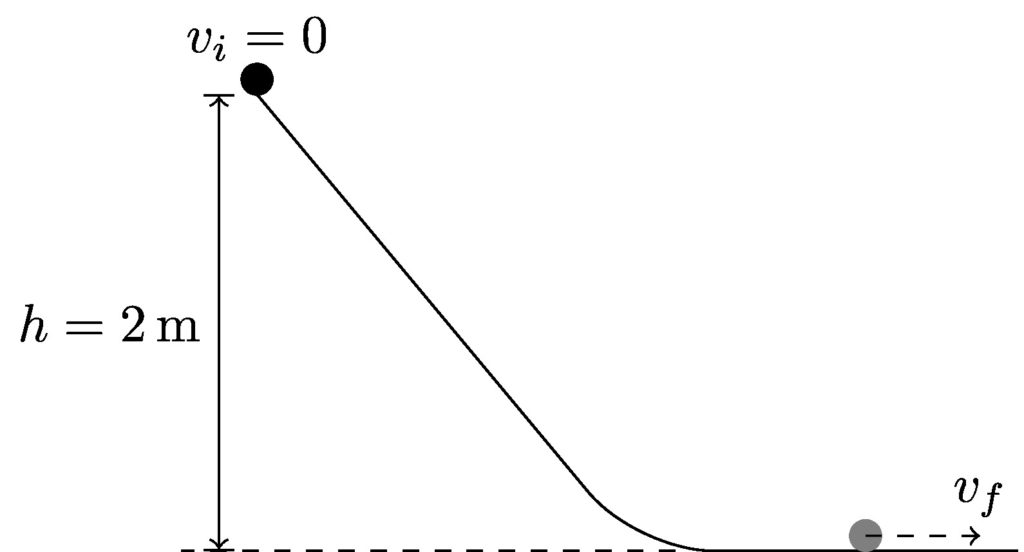
Step 2: Apply conservation of energy
Work from general to specific, starting from a fundamental principle of physics:
\[ E_i = E_f \]
“Initial energy” is the energy the cat has before it rolls down the ramp; it is initially at rest some height \(h\) above the ground, so it has gravitational potential energy. The “final energy” is the energy the cat has once it has reached the bottom of the ramp; it is now moving so it has kinetic energy. So we have \( E_i = U_g \) and \(E_f = K_t \). Since \( E_i = E_f\) we have
\[ U_g = K_t \]
Step 3: Solve
Now we can apply the specific expressions for gravitational potential energy and kinetic energy. Then we do the algebra to symbolically solve for the quantity we’re looking for (the final speed), and finally substitute values and calculate. I’ll show all the work from the very beginning.
\[
\begin{align*}
E_i &= E_f \\
U_g &= K_f \\
mgh &= \frac{1}{2}mv_f^2 \\
\frac{mgh}{m} &= \frac{1}{m}\left(\frac{1}{2}mv_f^2\right) \\
gh &= \frac{1}{2}v_f^2 \\
2(gh) &= 2\left(\frac{1}{2}v_f^2\right) \\
2gh &= v_f^2 \\
\sqrt{2gh} &= \sqrt{v_f^2} \\
\hookrightarrow v_f &= \sqrt{2gh} \\
&= \sqrt{2(9.8\ \textrm{m/s}^2)(2\ \textrm{m})} \\
&= 6.3\ \textrm{m/s}
\end{align*}
\]
Example 6.3
The cat from the previous example then goes up a 1 m tall ramp. What is its speed at the top of this ramp?

Now, the initial energy refers to the energy of the cat before going up the second hill, and the final energy is the energy of the cat when it is on top of the second hill. At this final point, it is some height above the ground, so it has gravitational potential energy, but it is also moving, so it also has kinetic energy.
\[
\begin{align*}
E_i &= E_f \\
K_i &= K_f + U_g \\
\frac{1}{2}mv_i^2 &= \frac{1}{2}mv_f^2 + mgh \\
\hookrightarrow v_f &= \sqrt{v_i^2 – 2gh} \\
&= \sqrt{(6.3\ \textrm{m/s})^2 – 2(9.8\ \textrm{m/s}^2)(1\ \textrm{m})} \\
&= 4.5\ \textrm{m/s}
\end{align*}
\]
Practice 6.5
Practice 6.6
Practice 6.7
Practice 6.8
Practice 6.9
Practice 6.10
Example 6.4
A disc with a radius 0.25 m is at rest on top of a 1 m tall hill. What is the speed of the wheel when it reaches the bottom?
(If you are drawing simplified drawings like I am, drawings for different problems may look basically the same—this is good! It tells you when you have already solved a similar problem! In this case, you can recycle the drawing used when the cat from the first example went down the ramp.)
For this example, we need to incorporate both translational and rotational kinetic energy.
\[
\begin{align*}
E_i &= E_f \\
U_g &= K_\textit{trans} + K_\textit{rot} \\
mgh &= \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2
\end{align*}
\]
For an object of radius \(r\) traveling at speed \(v\), the angular speed is \(\omega = \frac{v}{r}\). Additionally, the moment of inertia for a disc rotating around its center is \(I = \frac{1}{2}mr^2\). Making these substitutions gives us
\[
\begin{align*}
mgh &= \frac{1}{2}mv^2 + \frac{1}{2}\left(\frac{1}{2}mr^2\right)\left(\frac{v}{r}\right)^2 \\
2mgh &= mv^2 + \frac{1}{2}mv^2 \\
2gh &= \frac{3}{2}v^2 \\
\hookrightarrow v &= \sqrt{\frac{4}{3}gh} \\
&= 3.6\ \textrm{m/s}
\end{align*}
\]
Note that the mass and radius of the disk do not affect the final answer; any disk starting from rest at the top of a 1 m tall hill would be traveling at this speed when it reaches the bottom!