If you are attempting to push open a door, you do not push on it right next to the hinges. Even if you push with equal force near to the hinges, and then far from the hinges, you’ll find the door accelerates more quickly in one case than the other. (I encourage you to try pushing on the door close to the hinges to see how it feels.) When you are causing rotational motion, both the force and the where you apply the force are important.
11.1 Torque
Torque is what causes angular acceleration, just as force causes linear acceleration. The magnitude of any particular torque is given by the expression
\[ \tau = Fr\sin\theta \tag{11.1} \]
where \(F\) is the magnitude of the force, and \(r\) is the distance from where the force is applied to the axis of rotation. If you imagine \(r\) running in a straight line from the axis of rotation to the point where the force is applied, \(\theta\) is the angle between that line and the force, as shown below.
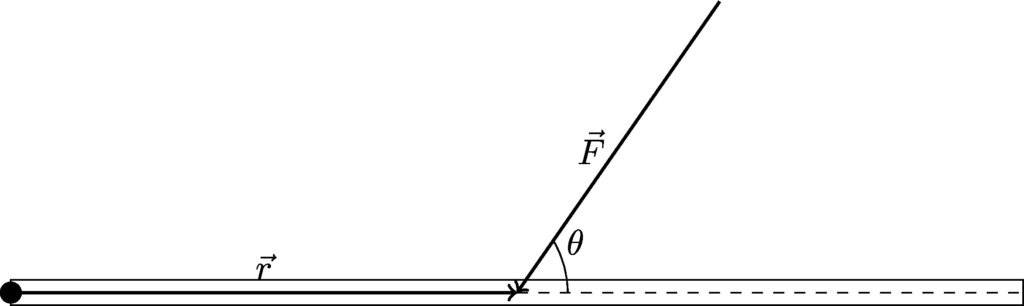
The unit of torque is the netwon-meter (N · m). Although this is the same unit as for energy, we do not refer to torque in units of joules. This is because of the difference in what that meter measures: for work and energy, the distance (we used \(d\)) is a distance traveled, or a displacement; for torque, the distance \(r\) is simply a measurement from one point to another on the object that is rotating—\(r\) does not measure any sort of displacement.
Torque is a vector quantity, so it needs a direction. We use the same convention as for rotation (chapter 5): torque is positive if it causes a counterclockwise angular acceleration, and negative if it causes a clockwise angular acceleration.
Example 11.1
Consider a ship whose wheel has a radius of 0.5 m. There are two people fighting for control of the ship. Nyneave is applying a force of 35 N tangentially to the wheel, and Lan is applying a force of 42 N at an angle of 30° relative to the radial direction. Nyneave is applying her force to make the wheel rotate in a clockwise direction; Lan is applying his force to oppose Nyneave. What is the net torque on the wheel? Which person gains control of the ship?
The net torque exerted on the wheel is the sum of the torque exerted by each person:
\[ \tau_\textit{net} = \tau_1 + \tau_2 \]
Call the wheel’s radius \(R\), and note how the direction of the applied force affects the torque.
\[
\begin{align*}
\tau_\textit{net} &= \tau_1 + \tau_2 \\
&= -RF_1\sin(90^\circ) + RF_2\sin(30^\circ) \\
&= -7\ \textrm{N}\cdot\textrm{m}
\end{align*}
\]
Since the net torque is negative, the wheel rotates clockwise. Nyneave wins, even though she is applying a smaller force—the direction relative to the axis of rotation is very important!