Chapter 10: Work

Posted onAuthordanroth

10.1: Work

I have a large cat whose mass is 7 kg. If he wants to jump up onto a table 1 m above the ground, his potential energy needs to increase by about 70 J \(\left(U = mgh \approx (7\ \textrm{kg})\left(10\ \textrm{m/s}^2\right)(1\ \textrm{m}) = 70\ \textrm{J}\right)\). In order to jump onto the table, chemical energy (stored in the cat’s muscles, and derived from the food he eats) was turned into potential energy.

Note that this is the cat’s weight \((mg)\) times the distance he traveled \((h)\). In general, the quantity of force times distance is known as the work done by that force:

\[ W = Fd \tag{10.1} \]

where \(F\) is the magnitude of the force applied, and \(d\) is the distance the object travels while the force is exerted.

The SI unit of work is the joule: \( 1\ \textrm{J} = 1\ \textrm{N}\cdot\textrm{m}\). (It is named in recognition of English brewer—and physicist—James Prescott Joule. He studied the related topics of work, heat, and energy.) This is the same unit as energy! Energy can be thought of as the ability to do mechanical work. Just like energy, work is a scalar quantity.

Example 10.1

You have three boxes. Each box has a height \(h = 0.5\ \textrm{m}\). Boxes \(A\) and \(B\) have a mass of 2 kg, and box \(C\) has a mass of 10 kg. All three boxes start on the ground:

Three boxes lay side-by-side on the ground, labeled A, B, and C. All three have the same height, but box C is wider than boxes A and B.
Three boxes on the ground

You then stack them in the following pile:

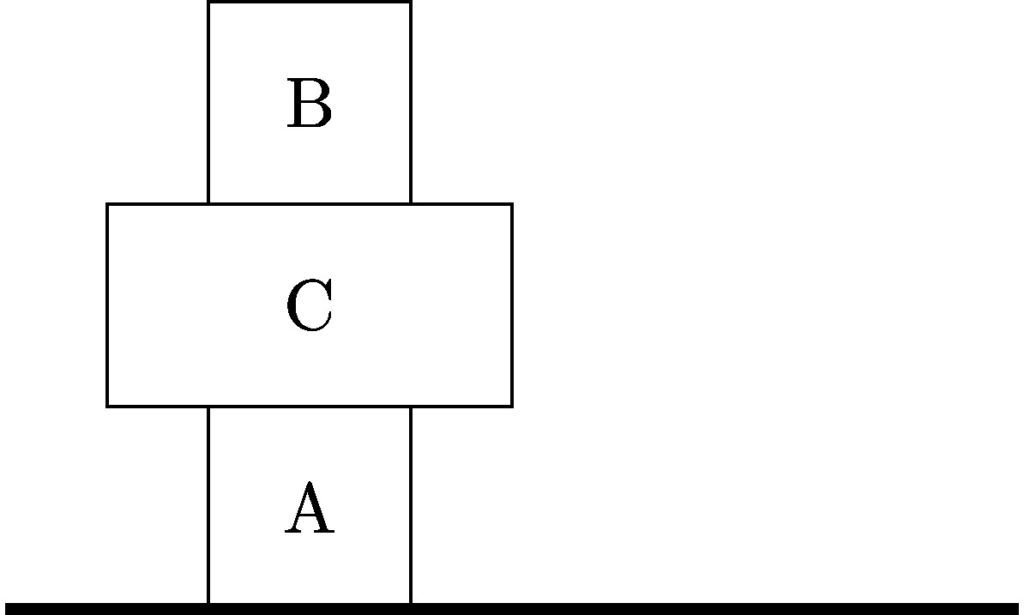
Three boxes are stacked. The box on the bottom is labeled A, the box in the middle is labeled C, and the box on top is labeled B. All three boxes have the same height, but box C is wider than the boxes A and B.
Three boxes stacked on top of one another

What is the total amount of work that you had to do, picking boxes \(B\) and \(C\) up one at a time?

In order to place box \(C\) onto box \(A\), you must apply a force equal to the weight of box \(C\), and move it a distance \(h\). The work to lift box \(C\) is

\[
\begin{align*}
W_c &= F^G_ch \\
&= m_cgh \\
&= (10\ \textrm{kg})\left(9.81\ \textrm{m/s}^2\right)(0.5\ \textrm{m}) \\
&= 49.1\ \textrm{J}
\end{align*}
\]

Box \(B\) must now be lifted a distance of \(2h\):

\[
\begin{align*}
W_b &= m_bg(2h) \\
&= (2\ \textrm{kg})\left(9.81\ \textrm{m/s}^2\right)(1\ \textrm{m}) \\
&= 19.6\ \textrm{J}
\end{align*}
\]

The total work done is

\[
\begin{align*}
W_\textit{total} &= W_b + W_c \\
&= 49.1\ \textrm{J} + 19.6\ \textrm{J} \\
&= 68.7\ \textrm{J}
\end{align*}
\]

Example 10.2

In the following figure, each block has the same height \(d\). The mass of each block is given in multiples of \(m\). Each stack has a total mass of \(11m\), but arranged differently. Determine which stack required the most work to assemble, and which required the least, if all the blocks initially start on the ground.

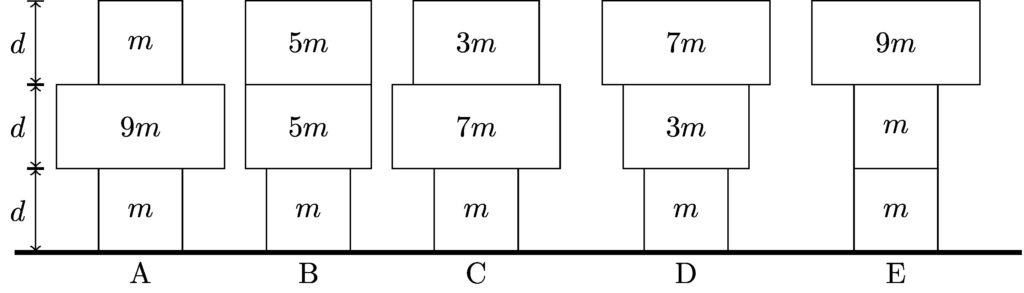
Five stacks of three boxes each. Each box has the same height, but some have different widths. Each box is labeled with its mass, in terms of the variable m. From left to right, the stacks are labeled with letters A, B, C, D, and E. In stack A, the bottom box has mass m, the middle box has mass 9m, and the top box has mass m. In stack B, the bottom box has mass m, the middle box has mass 5m, and the top box has mass 5m. In stack C, the bottom box has mass m, the middle box has mass 7m, and the top box has mass 3m. In stack D, the bottom box has mass m, the middle box has mass 3m, and the top box has mass 7m. In stack E, the bottom box has mass m, the middle box has mass m, and the top box has mass 9m.
Five stacks of three boxes. Each stack has the same total mass and height.

The process here is the same as it was for the previous example, except that we don’t have any values to work with. However, we can still compare the work done to assemble each stack.

For stack A, you lift a box with a mass of \(9m\) a distance \(d\), and a box with a mass \(m\) a distance \(2d\). The total work you did to assemble this stack was:

\[ W_A = (9m)gd + mg(2d) = 11mgd \]

Following a similar process for each stack, we find

\[
\begin{align*}
W_B &= (5m)gd + (5m)g(2d) & W_D &= (3m)gd + (7m)g(2d) \\
&= 15mgd & &= 17mgd \\
W_C &= (7m)gd + (3m)g(2d) & W_E &= mgd + (9m)g(2d) \\
&= 13mgd & &= 19mgd
\end{align*}
\]

And we see stack E requires the most work, and stack A requires least.

Practice 10.1