Chapter 9: Force

Posted onAuthordanroth

9.5 Mechanical equilibrium

An object (or group of objects) is said to be in mechanical equilibrium when the net force on it is zero. You could also describe this in terms of an object’s motion, considering Newton’s second law: an object is in mechanical equilibrium when its momentum is not changing, or in other words, when is not accelerating.

This describes many things that we encounter in the world around us. For example, take a look at any building—if any piece of a building has an acceleration other than zero, you do not want to be in or near that building!

Example 9.4

You and a friend are dragging a 75 kg box of potatoes across a floor at a constant speed. You are pushing with a force of 100 N. Your friend is pulling on a rope with a force of 200 N What is the force of kinetic friction that the floor exerts on the box if your friend is pulling up at a 25° angle? What is the normal force the ground exerts on the box?

FBD—Box
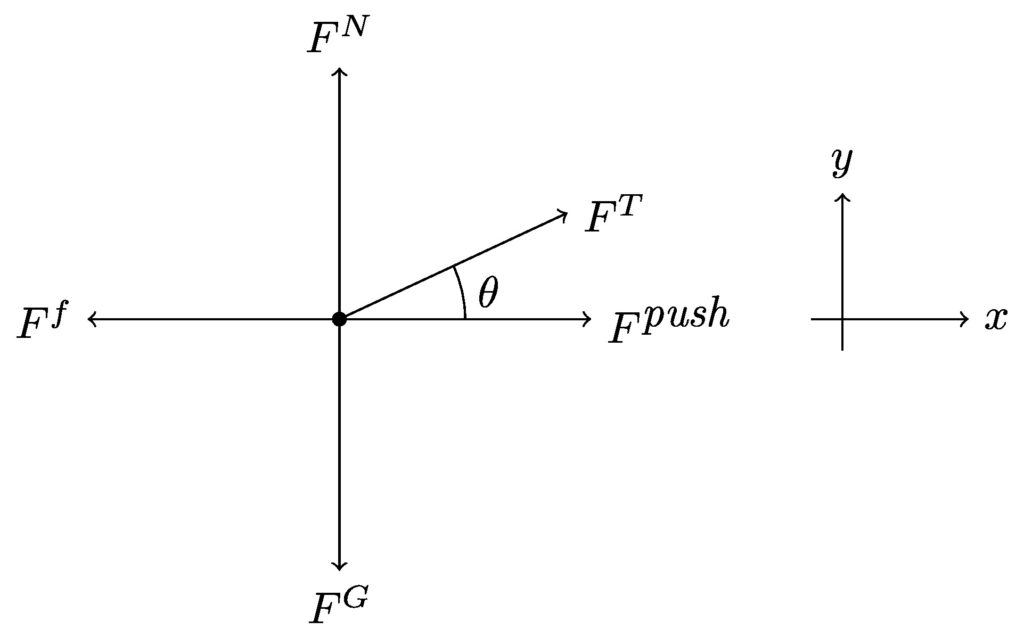
A dot has five arrows extending from it. One points directly to the right, labeled F superscript push. One points directly up, labeled F superscript N. One points directly to the left, labeled F superscript f. One points directly down, labeled F superscript G. The last arrow points up and to the right, labeled F superscript T. The angle this arrow makes with the horizontal is labeled with a Greek lowercase theta. To right side is another set of two arrows; one points directly to the right, labeled x; the other points directly up, labeled y.
Free body diagram for the box of potatoes
Newton’s second law:

\[
\begin{align*}
F_\textit{net,x} &= ma_x & F_\textit{net,y} &= ma_y \\
F^T_x + F^\textit{push} – F^f &= m(0) & F^N + F^T_y – F^G &= m(0) \\
F^T\cos\theta + F^\textit{push} – F^f &= 0 & F^N + F^T\sin\theta – mg &= 0 \\
F^f &= F^T\cos\theta – F^\textit{push} & F^N &= mg – F^T\sin\theta \\
&= (200\ \textrm{N})\cos(25^\circ) – 100\ \textrm{N} & &= (75\ \textrm{kg})\left(9.81\ \textrm{m/s}^2\right) – (200\ \textrm{N})\sin(25^\circ) \\
&= 81.3\ \textrm{N} & &= 651\ \textrm{N}
\end{align*}
\]

Example 9.5

A bag full of books \(\left(m = 5.3\ \textrm{kg}\right)\) is resting on a table. You attach a spring, which has a spring constant of 150 N/m to the bag, and pull horizontally. The spring is stretched 2.5 cm just before the bag begins to move. What is the force of static friction that the table exerts on the bag?

FBD—Bag
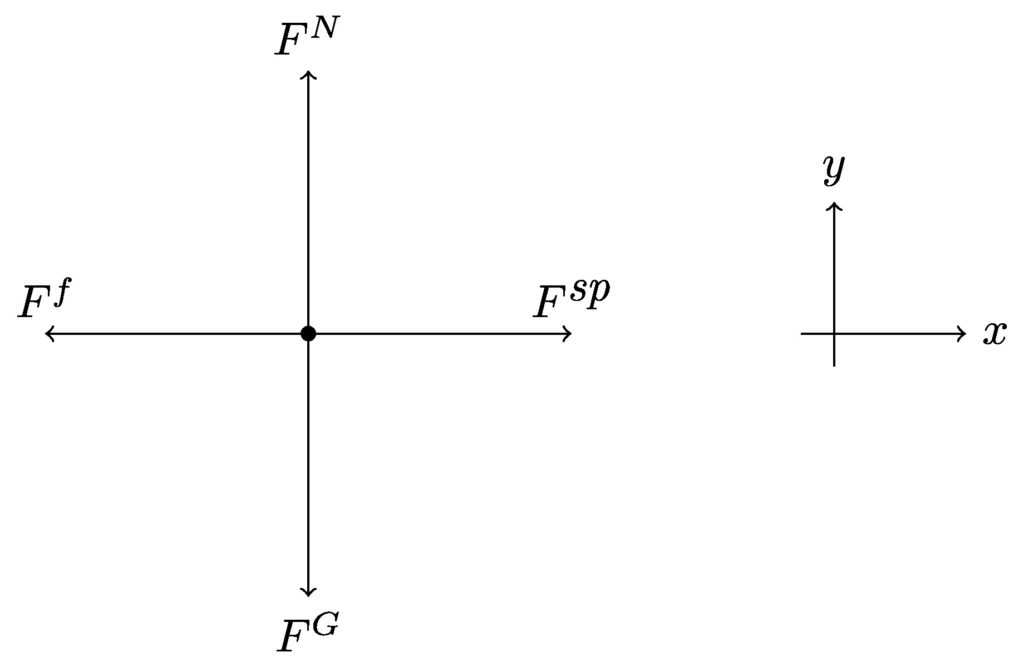
A dot has four arrows extending from it. One points directly to the right, labeled F superscript sp. One points directly up, labeled F superscript N. One points directly left, labeled F superscript f. One points directly down, labeled F superscript G. To the right is another set of arrows; one points directly right, labeled x; the other points directly up, labeled y.
Free body diagram for the bag of books
Newton’s second law

Just before the bag begins to move, its acceleration is zero.

\[
\begin{align*}
F_\textit{net,x} &= ma_x \\
F^\textit{sp} – F^f &= m(0) \\
kx – F^f &= 0 \\
F^f &= kx \\
&= (150\ \textrm{N/m})(2.5 \times 10^{-2}\ \textrm{m}) \\
&= 3.75\ \textrm{N}
\end{align*}
\]

Example 9.6

A flower basket is hanging from two wires. One wire is attached at a right angle to a wall, and the other is attached to the ceiling at an angle of 30° to the horizontal. The mass of the basket is 6 kg. What is the tension in each wire?

FBD—Flower basket
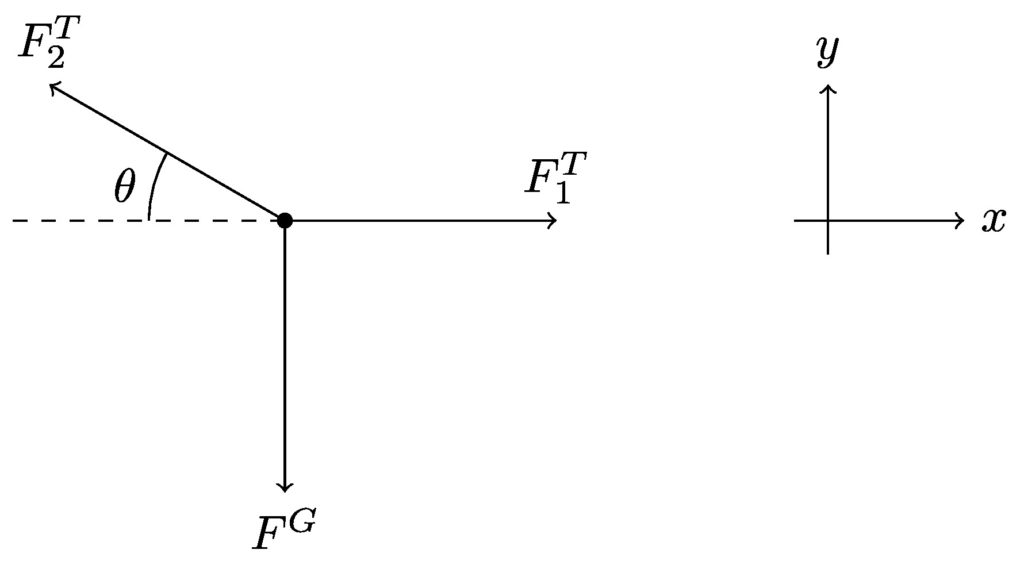
A dot has three arrows extending from it. One points directly to the right, labeled F superscript T subscript 1. One points straight down, labeled F superscript G. One points to the left and up, labeled F superscript T subscript 2. A dashed line extends from the dot directly to the left; the angle between this horizontal dashed line and the angled arrow is labeled with a lowercase Greek theta. To the right is another set of arrows; one points directly to the right, labeled x; the other points directly up, labeled y.
Free body diagram for the flower basket

In the previous problems, we could find out everything we wanted by just using the \(x\) or \(y\) components of the forces. For this problem, we will need to solve a system of two equations to find the tension in each wire.

Newton’s second law

Now, we’ll find \(F^T_2\) using the \(y\) components of the forces, and do a substitution to find \(F^T_1\).

\[
\begin{align*}
F^T_1 &= F^T_2\cos\theta & F^T_2 &= \frac{mg}{\sin\theta} \\
&= \left(\frac{mg}{\sin\theta}\right)\cos\theta & &= \frac{(6\ \textrm{kg})\left(9.81\ \textrm{m/s}^2\right)}{\sin(30^\circ)} \\
&= \left(\frac{(6\ \textrm{kg})\left(9.81\ \textrm{m/s}^2\right)}{\sin(30^\circ)}\right)\cos(30^\circ) & &= 117.7\ \textrm{N} \\
&= 101.9\ \textrm{N}
\end{align*}
\]

You’ll notice I algebraically substituted \(\frac{mg}{\sin\theta}\) for \(F^T_2\), rather than simply using the value 117.7 N. I do this for two reasons: you can often discover interesting relationships between the variables by focusing on the physical quantities rather than specific values; and you avoid errors that arise from rounding.

Practice 9.6