6.4 Potential energy
While kinetic energy is energy that is associated with motion, potential energy is associated with an object’s position. It can be thought of as stored energy that has the potential to gain kinetic energy. We will focus on two ways of storing energy: lifting an object up to some height, and stretching or compressing a spring.
6.4.1 Gravitational potential energy
If you lift an object into the air, it will gain kinetic energy when you let go and it begins to fall. This kinetic energy was converted from gravitational potential energy. Gravitational potential energy is given by
\[
U_g = mgh \tag{6.5}
\]
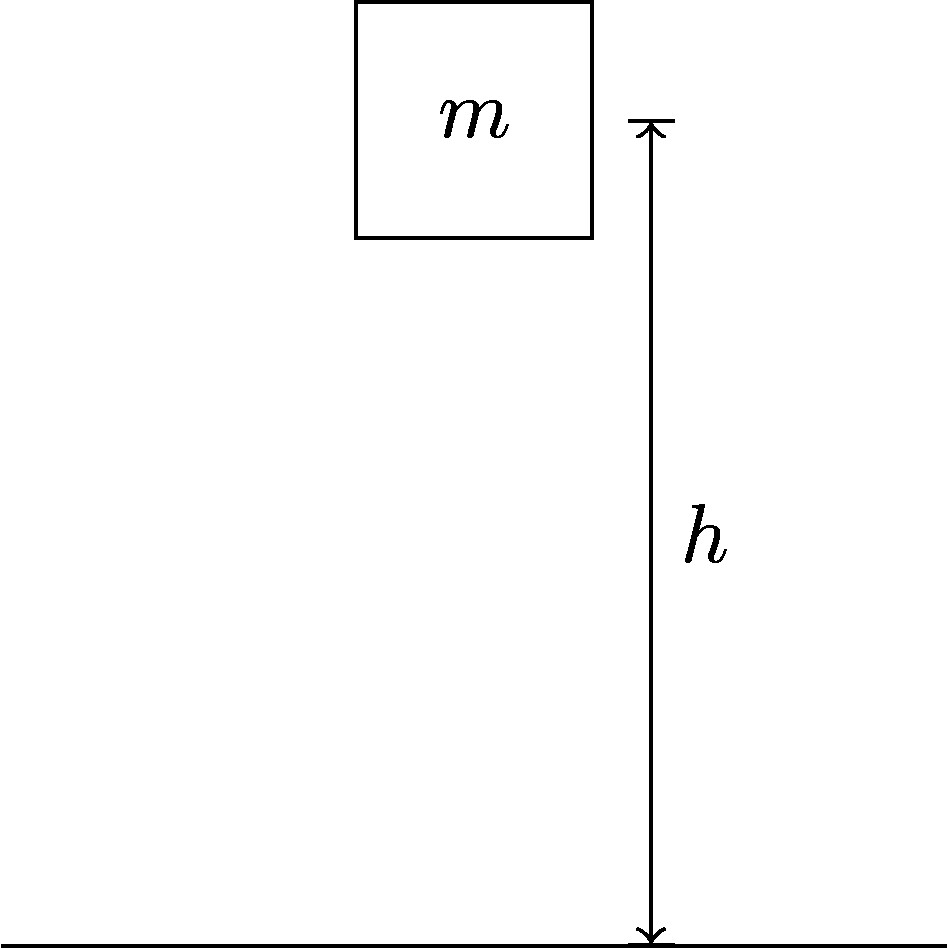
where \(m\) is the mass of the object, \(h\) is the height it has been lifted up to, as shown in the figure below, and \(g = 9.81\) m/s2 is the strength of Earth’s gravitational field (when you are close to the surface). We’ll see in chapter 12 that this is also the acceleration of an object in free fall.
Universal gravitation
As far back as the 1600s, precise measurements were made which determined that the strength of gravity is different in different locations, with a large factor being elevation above sea level. Isaac Newton derived a precise mathematical relationship between the strength of a gravitational field, Earth’s mass, and the distance from the center of the Earth:
\[
g = G \frac{M}{d^2} \tag{6.6}
\]
where \(M\) is the mass of Earth, \(d\) is the distance from your location to the center of Earth, and \(G\) is a fundamental constant of the universe known as the gravitational constant. Newton did not know the precise value for \(G\): he derived the general relationship between \(g\), \(M\), and \(d\), and the values (in any system of units) were experimentally determined later.
In SI units, \(M = 5.972 \times 10^{24}\) kg and \(G = 6.67 \times 10^{-11}\) m3/kg·s2. On average, at sea level, \(d = 6.371 \times 10^6\) m; substituting these values gives us \(g = 9.81 \approx 10\) m/s2.
6.4.2 Spring potential energy
The energy stored in a compressed or stretched spring is given by
\[
U_\textit{sp} = \frac{1}{2}kx^2 \tag{6.7}
\]
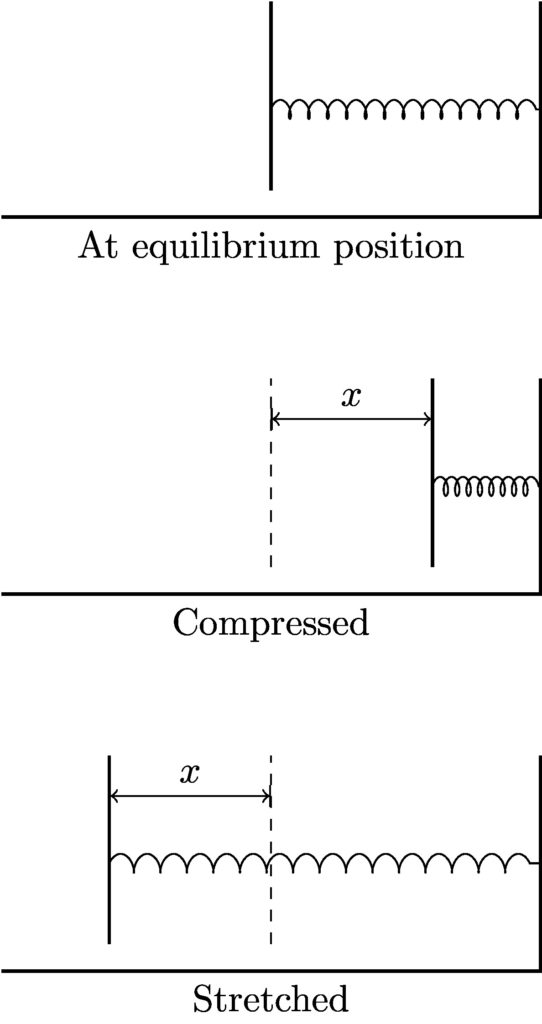
The spring constant \(k\) depends on the particular spring you are using, and has units of J/m2. The distance \(x\) is measured relative to the equilibrium position of the spring, as shown in the figure below.