1.3 Pythagorean theorem
In addition to the three trig functions, which relate two sides and an angle, we also have a relationship between the three sides. This is known as the Pythagorean theorem. For a right triangle with sides a and b, and hypotenuse c, the three lengths have the relationship
\[
a^2 + b^2 = c^2 \tag{1.4}
\]
While in the Western science tradition we name this relationship after the Greek mathematician Pythagoras, it had been discovered earlier by the Mesopotamians, Indians and Chinese. It is unclear if one particular culture made the discovery first and others learned from them, or if it was discovered independently by each. It is likely that the Greeks learned about it from the Mesopotamians, by way of Egyptians.1 It is also unclear that Pythagoras himself recorded a proof of this theorem. Pythagoras founded a community of philosophers and mathematicians, all of whom wrote under the name of Pythagoras.2
Lacking a commonly-recognized alternative, I’ll continue to refer to this relationship by the name “the Pythagorean theorem.” It provides us another tool to use when working with right triangles.
Example 1.2
In the triangle below, what is cos(𝜃)?
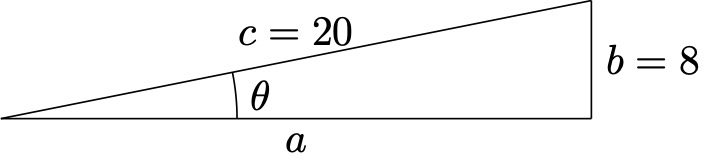
In order to find cos(𝜃), we need to know the side adjacent to the angle. Do this using the Pythagorean theorem.
\[
\begin{align*}
a &= \sqrt{c^2 – b^2} \\
&= \sqrt{20^2 – 8^2} \\
&= \sqrt{336}
\end{align*}
\]
Now that we know the length of the adjacent side, we can find the cosine of the angle:
\[
\begin{align*}
\cos(\theta) &= \frac{a}{c} \\
&= \frac{\sqrt{336}}{20} \\
&= 0.927
\end{align*}
\]
Example 1.3
What is tan(𝜃) for a triangle where cos(𝜃) = 3/4?
If cos(𝜃) = 3/4, then leg of the triangle adjacent to 𝜃 has a length of 3, and the hypotenuse has a length of 4. Using the Pythagorean theorem tells us the leg opposite from 𝜃 is
\[
\begin{align*}
b &= \sqrt{c^2 – a^2} \\
&= \sqrt{16 – 9} \\
&= \sqrt{7}
\end{align*}
\]
We then have
\[
\begin{align*}
\tan(\theta) &= \frac{\sqrt{7}}{3} \\
&= 0.882
\end{align*}
\]
(Technically, it’s just that the ratio of these two sides is 3/4, but the ratio is all that really matters. If you make the triangle bigger by multiplying all sides by the same number, you’ll have the same ratio even though the sides themselves are different. But the outcome of the problem would be the same. For example, you could say the opposite side has a length of 6 and the hypotenuse has a length of 8. You would then find the adjacent side has a length of 2√7, but you would still find tan(𝜃) = 0.882. For the purposes of solving this sort of problem, we can stick with the simplest case and take the given values as the side lengths.)
Practice 1.6
Practice 1.7
Practice 1.8
1The Pythagorean Theorem: The story of its power and beauty, by Alfred S. Posamentier
2Hypatia’s Heritage: A history of women in science from antiquity through the nineteenth century, by Margaret Alic.