We encountered prefix notation earlier when we looked at various types of representation. In prefix notation, the operator goes before the operands:
\((+\; 2\; 3)\)This means apply the plus operator to 2 and 3… or does it? Yes, once we’ve read the whole expression we know it does, but remember the prefix problem? We’d prefer to know what we’re supposed to do even before we’ve read the whole expression, so let’s keep it a little vaguer than that, and agree that all it means is that we’re going to apply the plus operator to the next two arguments. Maybe they’re numbers, maybe they’re sub-expressions that will also be needed to be evaluated, but we’ll deal with that when we need to.
Remember the difference between syntax and semantics? Take a look at these three instructions:
System.out.println("Hello");
cout << "Hello" << endl;
printf("Hello\n");
We have Java, C++ and C code, all doing the same thing, writing the word “Hello” on the screen. That’s the semantics; the syntax is all about having the right brackets or semi colons, or that weird << thing that C++ uses. Think of this as a design task: all we want to do is have the word “Hello” written to the screen, without worry about exactly how that will be done. However, we do have to write it in some form, and that’s why we use what is called abstract syntax. This is a representation that is independent of any language and, if we design our code in it, then we can easily translate it into programming language with a (hopefully) easy translation process. We can design once and deploy as many times as we want, possibly using different languages for different computers, and certainly choosing the language that best suits the problem we’re trying to solve.
Are we writing a piece of code for a browser based game? Then let’s generate JavaScript. Are we doing some simple Machine Learning? Maybe let’s go for Python.
This is why we want to separate the what from the how. We focus on what the program is actually doing before we worry about how it will achieve this.
If abstract syntax doesn’t have a language, when what does it look like? In this course, we’ll use Abstract Syntax Trees (ASTs). These are diagrams of mathematical expression. Take our (+ 2 3) expression, for example, and we get:
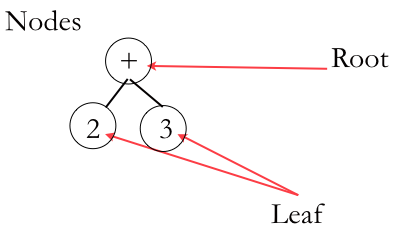
A simple Abstract Syntax Tree. Each operator and operand from an expression becomes a node.
The operator is at the top, the parent and the operands are the children or the leaves. Here’s a slightly more complex one:
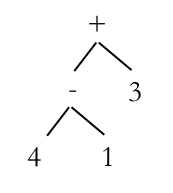
An AST with multiple levels.
This time we have multiple levels, because there’s another operator in the tree. The top level (the +) is Level 0, the next Level 1 and so on. To evaluate an AST, we find the deepest node and evaluate it. In this case it is (- 4 1), which gives us 3, so we redraw our AST to give us:
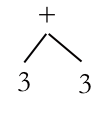
The AST after the deepest operator has been evaluated.
Now the deepest operator is the +, so we just evaluate (+ 3 3) and we get 6, our final answer. What’s great about these is that they all work the same way. Look this next example. We just go to the deepest operator and keep working our way out. In this case, there are two on the same level, but it doesn’t matter which one we do first, although normally we go from left to right, just to make it clearer when we’re showing all our work.
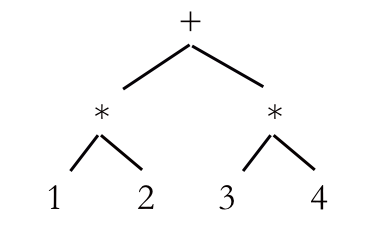
A slightly more complex AST. We start with the * signs and work our way out.
Let’s try to evaluate some of these:
Notice that the ASTs have a very similar structure to prefix notation: the operator is the parent and the operands and are the child notes. Let’s look at some more complex prefix expressions, for example the one from the slightly more complex AST above (+ (* 1 2) (* 3 4) ), and work through it character by character. We read the + and here’s what happens:
- Read +
- Get the first argument
- Get the second argument
- Add them
The first argument is (* 1 2), which means almost the same thing, except this time we’ll multiple the arguments once we have them:
- Read *
- Get the first argument
- Get the second argument
- Multiply them
We evaluate this to 3 and then move onto (* 3 4) which, again, give us:
- Read *
- Get the first argument
- Get the second argument
- Multiply them
Notice how we’re repeating the same thing? Even when we change from + to *, the steps are virtually identical, except for the last one where we carry out the operation. Remember how the section on Locality of Reference discussed how it’s often more efficient to execute the same small thing multiple times than it is to execute something large? This is one very nice property of prefix notation. Not only do we not have to have everything read before we evaluate it, but we can evaluate it using the same set of steps for every operator. This algorithm finds the most deeply nested sub expression and evaluates that first.
Let’s one last example. To evaluate this expression (+ (* (/ 2 1) 3) 4), we evaluate the (/ 2 1) first to get:
(+ (* 2 3) 4)
Next we do (* 2 3) and that leaves us with (+ 6 4) which gives 10.
What does all this give us? We have ASTs which have no syntax and are going to be used for design, and we have prefix notation which is a fast and convenient way to evaluate them. All we need now is a way to convert from one to the other. Fortunately, there is a nice simple algorithm to do that for us which will see in the next section!
In the meantime, do so more practice with evaluate ASTs: