We’ve already seen local and global variables in Racket.
> (define x 2) > (define addx (lambda (y) (+ y x)))
In the function addx the variable y is local and x is global.
Let’s try applying the function to the value 4. As y is the parameter, it gets the value 4, which is added to the value of x, which is 2.
> (addx 4) 6
Here’s what it looks like using syntax trees. Remember, a \(\beta\) conversion is when we bring the value in for a parameter.
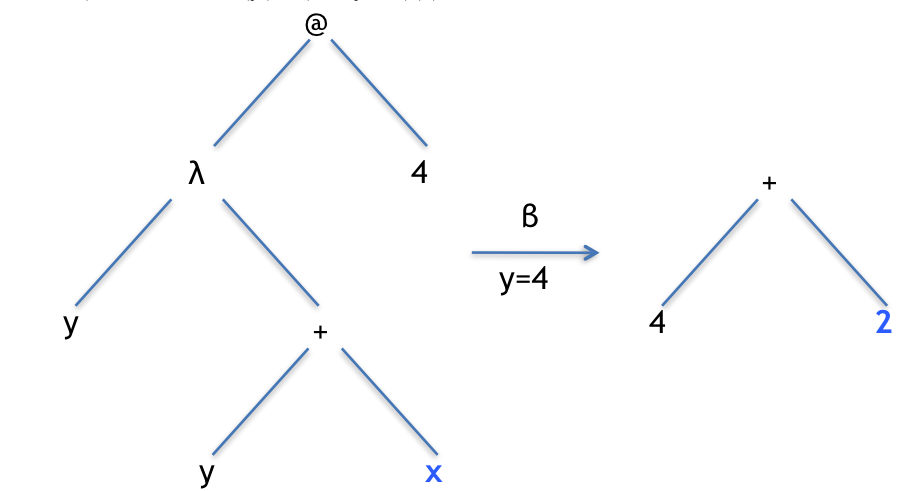
Applying the addx function to an argument. Notice that x is a global variable so we don’t explicitly pass a value to it (because it has already been defined).
This is fairly straightforward because there’s just one function, and it is a fairly simple one, but this is about to get very complex, so let’s build ourselves some machinery to analyse these functions. We’ll start off with some shorthand:
λx. E
is a function that takes exactly one argument. Note that we don’t care what the function body actually does, as all we’re interested in is keeping track of variables
Similarly:
λx. E F
is also a function that takes exactly one argument, but this time there are two distinct parts to the function body, for example, if we had something like this (λx. + 1 2) we could say that
\(\lambda x. + x\; y \equiv \lambda x. E \)because E = + x y
We can also say that
\(\lambda x. + x\; y \equiv \lambda x. E\; F \)because E = + x and F = y. However, we could equally say that
\(\lambda x. + x\; y \equiv \lambda x. E\; F \)because E = + and F = x y, because there are still two parts. What we could not say is that F = + x y, because then there would be nothing for E.
Here’s one last example:
\(\lambda x. x \equiv \lambda x. E \)because E = x, but
\(\lambda x. x \not\equiv \lambda x. E\; F \)because there’s only one item in the function body.
In λ calculus, a local variable is referred to as a bound variable, so for example, x is bound in (λx. + x y) because it is in the body of the function and in the parameter list. What about y? It’s clearly not bound because it’s value is coming from somewhere else, however, for reasons that we’ll see shortly it isn’t necessarily a global variable, so we refer to it as a free variable.
The next section will look how formal steps to identify free and bound variables which will make our lives easier when dealing with complex functions and expressions.